Understanding Media Saturation in Marketing Mix Models#
One of the most important concepts in Marketing Mix Modeling (MMM) is media saturation - the phenomenon where the incremental impact of advertising spend diminishes as spending increases. Understanding saturation is crucial for making optimal budget allocation decisions.
This tutorial explores two complementary ways to visualize and understand media saturation after fitting an MMM.
Direct/Marginal Contribution (
saturation_scatterplot) - Shows the relationship between spend and contribution at each time point.Total Contribution over Spend Share (
mmm.plot.channel_contribution_grid) - Shows how total contribution changes as you scale overall spend
Warning
These two visualizations answer different questions and are often confused. This tutorial clarifies the distinction and provides guidance on when to use each.
Setup and Data Preparation#
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import preliz as pz
import seaborn as sns
from pymc_extras.prior import Prior
from pymc_marketing.mmm import GeometricAdstock, LogisticSaturation
from pymc_marketing.mmm.multidimensional import MMM
from pymc_marketing.paths import data_dir
az.style.use("arviz-darkgrid")
plt.rcParams["figure.figsize"] = [12, 7]
plt.rcParams["figure.dpi"] = 100
%load_ext autoreload
%autoreload 2
%config InlineBackend.figure_format = "retina"
/Users/juanitorduz/Documents/pymc-marketing/pymc_marketing/mmm/multidimensional.py:218: FutureWarning: This functionality is experimental and subject to change. If you encounter any issues or have suggestions, please raise them at: https://github.com/pymc-labs/pymc-marketing/issues/new
warnings.warn(warning_msg, FutureWarning, stacklevel=1)
/Users/juanitorduz/Documents/pymc-marketing/pymc_marketing/mmm/time_slice_cross_validation.py:32: UserWarning: The pymc_marketing.mmm.builders module is experimental and its API may change without warning.
from pymc_marketing.mmm.builders.yaml import build_mmm_from_yaml
seed: int = sum(map(ord, "mmm"))
rng: np.random.Generator = np.random.default_rng(seed=seed)
Understanding the Saturation Curve#
Before diving into the visualizations, let’s understand what a saturation curve represents. In this notebook we consider the logistic saturation function:
Where:
\(x\) is the (adstocked) media spend
\(\beta\) is the saturation ceiling - the maximum contribution a channel can achieve
\(\lambda\) is the efficiency parameter - how quickly the curve approaches saturation
PyMC-Marketing provides the LogisticSaturation class to work with this transformation. This class allows us to:
Define custom priors for the parameters
Sample from the prior distributions
Visualize the saturation curves
Let’s explore how to use this class and understand how the parameters affect the saturation curve.
# Create a LogisticSaturation instance with default priors
saturation = LogisticSaturation()
# View the default priors for the saturation parameters
saturation.default_priors
{'lam': Prior("Gamma", alpha=3, beta=1), 'beta': Prior("HalfNormal", sigma=2)}
Note
PyMC-Marketing provides many other saturation functions like HillSaturation and MichaelisMentenSaturation.
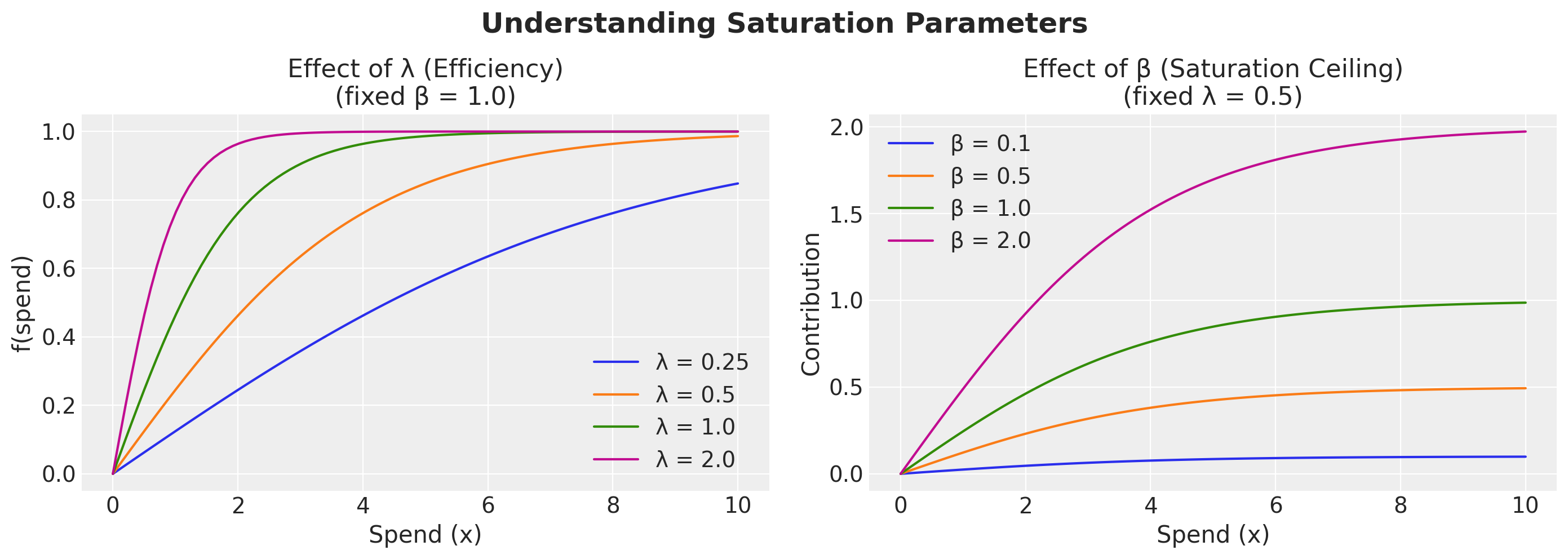
Before doing any sampling, let’s get an intuition of how the parameters affect the saturation curve.
/var/folders/cm/3dzy9rdd5s3672z0s1brjkvh0000gn/T/ipykernel_24206/1421674359.py:32: UserWarning: The figure layout has changed to tight
plt.tight_layout()
Key observations:
Higher \(\beta\) → Higher maximum contribution (the curve’s ceiling)
Higher \(\lambda\) → Faster saturation (the curve rises more steeply but plateaus sooner)
Next, we show how to sample from the prior distributions and visualize the saturation curves.
# Sample from the prior distributions
prior = saturation.sample_prior(random_seed=rng)
# Sample the saturation curve across a range of spend values
curve = saturation.sample_curve(prior, num_points=500, max_value=3)
# Plot the saturation curve with uncertainty (HDI and samples)
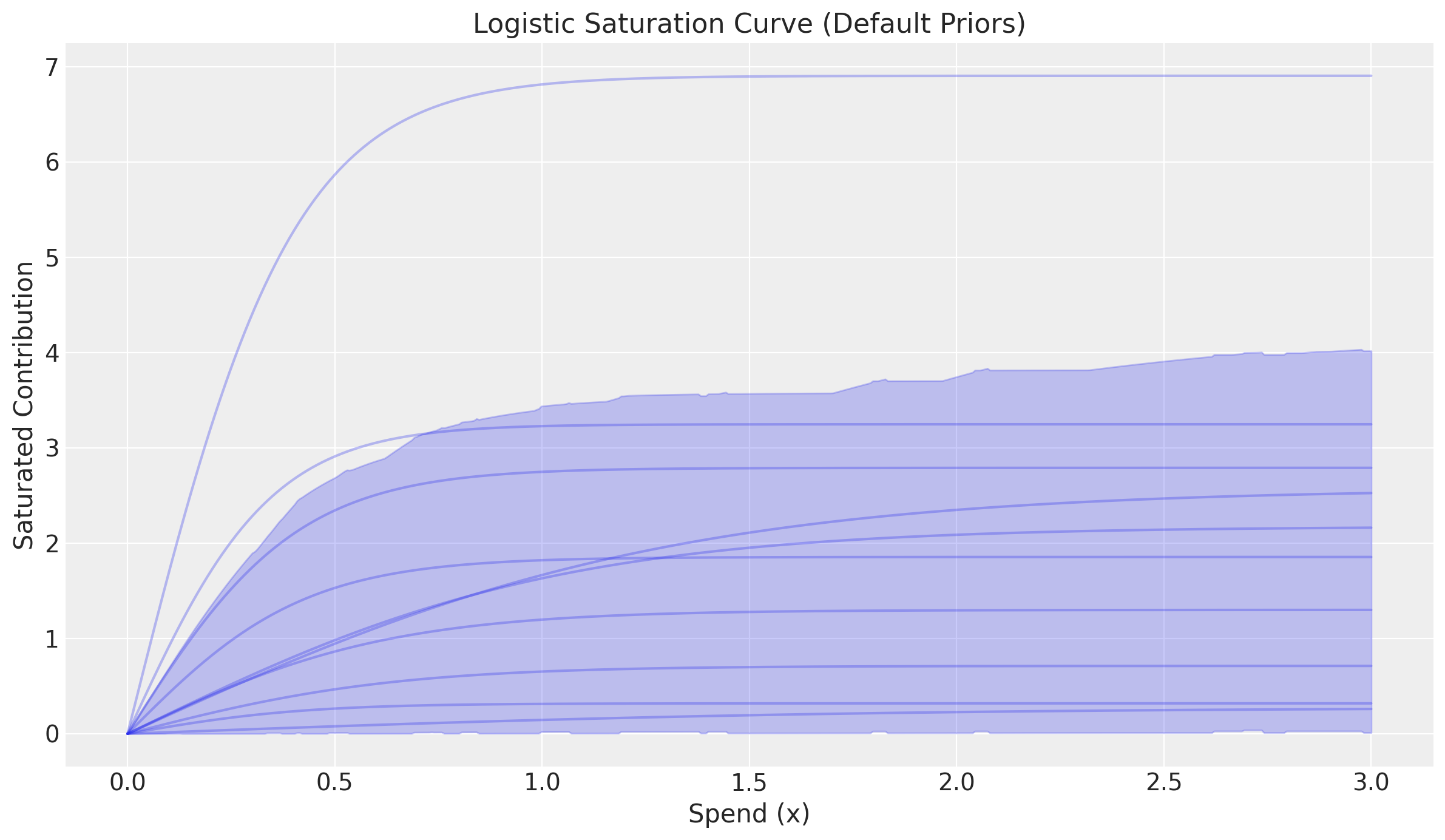
fig, axes = saturation.plot_curve(curve, random_seed=rng)
axes[0].set(
xlabel="Spend (x)",
ylabel="Saturated Contribution",
title="Logistic Saturation Curve (Default Priors)",
)
plt.tight_layout()
Sampling: [saturation_beta, saturation_lam]
Sampling: []
/var/folders/cm/3dzy9rdd5s3672z0s1brjkvh0000gn/T/ipykernel_24206/1957016988.py:14: UserWarning: The figure layout has changed to tight
plt.tight_layout()
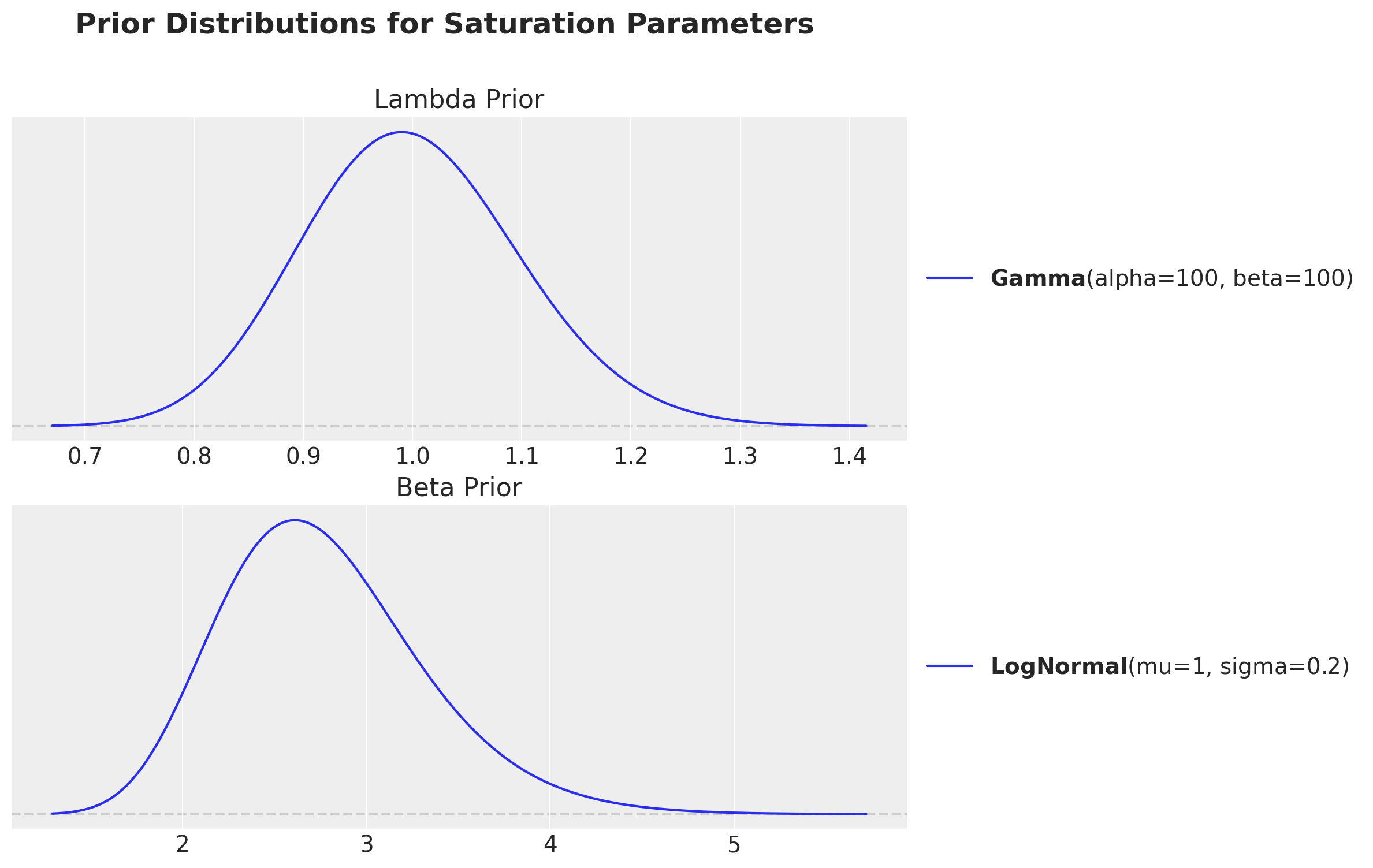
Let’s do the same thing with more tight priors.
fig, ax = plt.subplots(
nrows=2,
ncols=1,
figsize=(10, 8),
sharex=False,
sharey=False,
layout="constrained",
)
pz.Gamma(alpha=100, beta=100).plot_pdf(ax=ax[0])
ax[0].set(title="Lambda Prior")
pz.LogNormal(mu=1, sigma=0.2).plot_pdf(ax=ax[1])
ax[1].set(title="Beta Prior")
fig.suptitle(
"Prior Distributions for Saturation Parameters", fontsize=18, fontweight="bold"
);
# Create a LogisticSaturation instance with default priors
saturation = LogisticSaturation(
{
"lam": Prior("Gamma", alpha=100, beta=100),
"beta": Prior("LogNormal", mu=1, sigma=0.2),
}
)
# Sample from the prior distributions
prior = saturation.sample_prior(random_seed=rng)
# Sample the saturation curve across a range of spend values
curve = saturation.sample_curve(prior, num_points=500, max_value=3)
# Plot the saturation curve with uncertainty (HDI and samples)
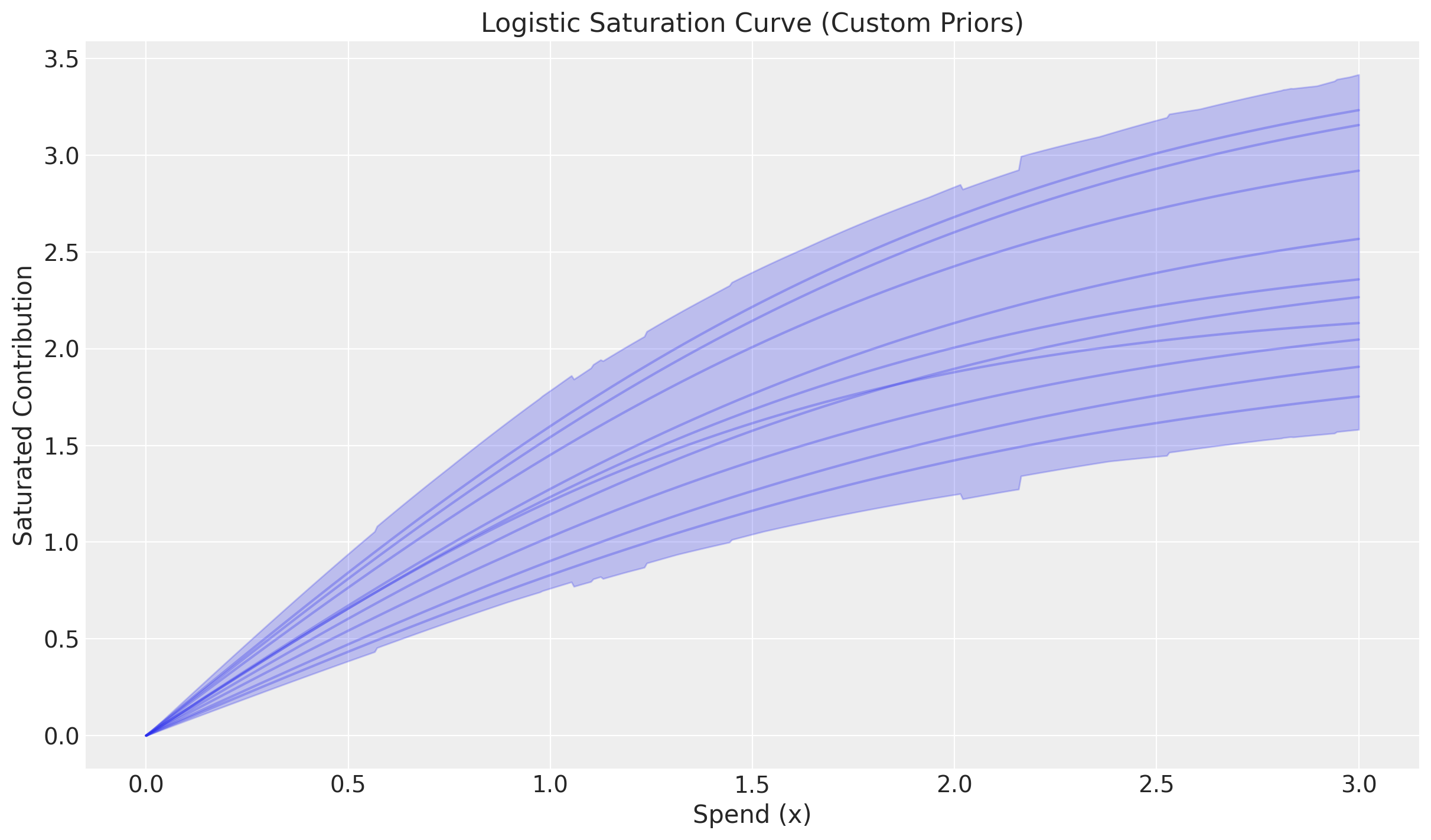
fig, axes = saturation.plot_curve(curve, random_seed=rng)
axes[0].set(
xlabel="Spend (x)",
ylabel="Saturated Contribution",
title="Logistic Saturation Curve (Custom Priors)",
);
Sampling: [saturation_beta, saturation_lam]
Sampling: []
We clearly see the samples are more concentrated around the mean.
We now see how these saturation curves are used in an MMM and how to extract business insights from them.
Read Data#
We use the same data as in the MMM Multidimensional Example Notebook tutorial.
data_path = data_dir / "mmm_multidimensional_example.csv"
data_df = pd.read_csv(data_path, parse_dates=["date"])
data_df.head(10)
| date | geo | x1 | x2 | event_1 | event_2 | y | |
|---|---|---|---|---|---|---|---|
| 0 | 2022-06-06 | geo_a | 5527.640078 | 0.000000 | 0 | 0 | 2647.596355 |
| 1 | 2022-06-06 | geo_b | 8849.257500 | 8063.918386 | 0 | 0 | 682.406280 |
| 2 | 2022-06-13 | geo_a | 6692.655692 | 0.000000 | 0 | 0 | 5020.823907 |
| 3 | 2022-06-13 | geo_b | 9073.817994 | 9354.014585 | 0 | 0 | 3753.104897 |
| 4 | 2022-06-20 | geo_a | 7124.016733 | 0.000000 | 0 | 0 | 6184.322132 |
| 5 | 2022-06-20 | geo_b | 7867.854558 | 5608.112521 | 0 | 0 | 3329.279953 |
| 6 | 2022-06-27 | geo_a | 7725.169902 | 0.000000 | 0 | 0 | 5446.374631 |
| 7 | 2022-06-27 | geo_b | 9712.332359 | 11760.981800 | 0 | 0 | 7544.192188 |
| 8 | 2022-07-04 | geo_a | 8545.792935 | 0.000000 | 0 | 0 | 10058.970814 |
| 9 | 2022-07-04 | geo_b | 6747.884370 | 6774.114961 | 0 | 0 | 2359.259385 |
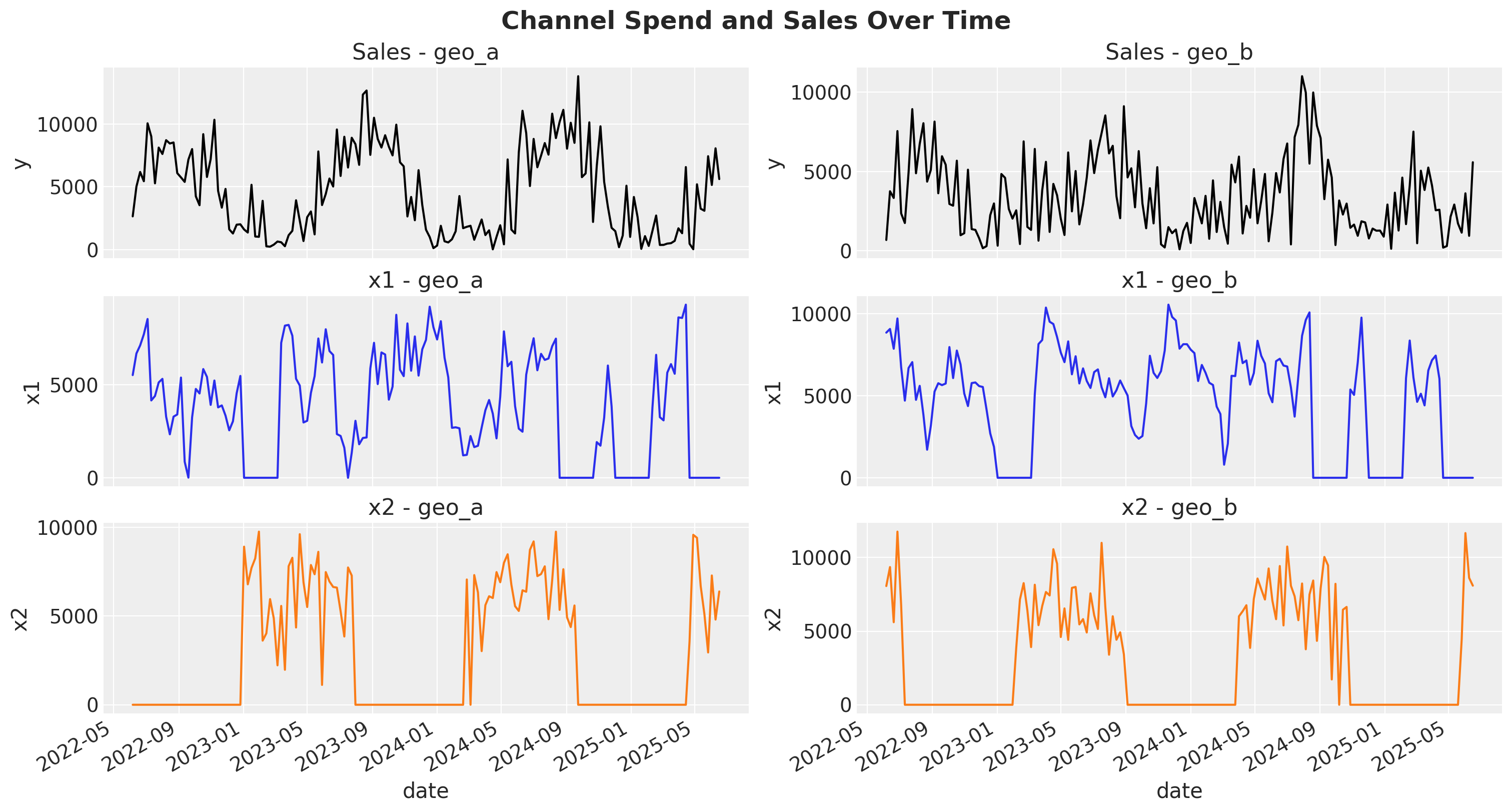
Let’s visualize the spend and sales data for each channel and geography.
fig, axes = plt.subplots(
nrows=3,
ncols=2,
figsize=(15, 8),
sharex=True,
sharey=False,
layout="constrained",
)
for i, geo in enumerate(["geo_a", "geo_b"]):
geo_data = data_df.query("geo == @geo")
for j, channel in enumerate(["x1", "x2"]):
sns.lineplot(
x=geo_data["date"],
y=geo_data[channel],
color=f"C{j}",
ax=axes[j + 1, i],
)
axes[j + 1, i].set_title(f"{channel} - {geo}")
sns.lineplot(
x=geo_data["date"],
y=geo_data["y"],
color="black",
ax=axes[0, i],
)
axes[0, i].set_title(f"Sales - {geo}")
fig.autofmt_xdate()
fig.suptitle("Channel Spend and Sales Over Time", fontsize=18, fontweight="bold");
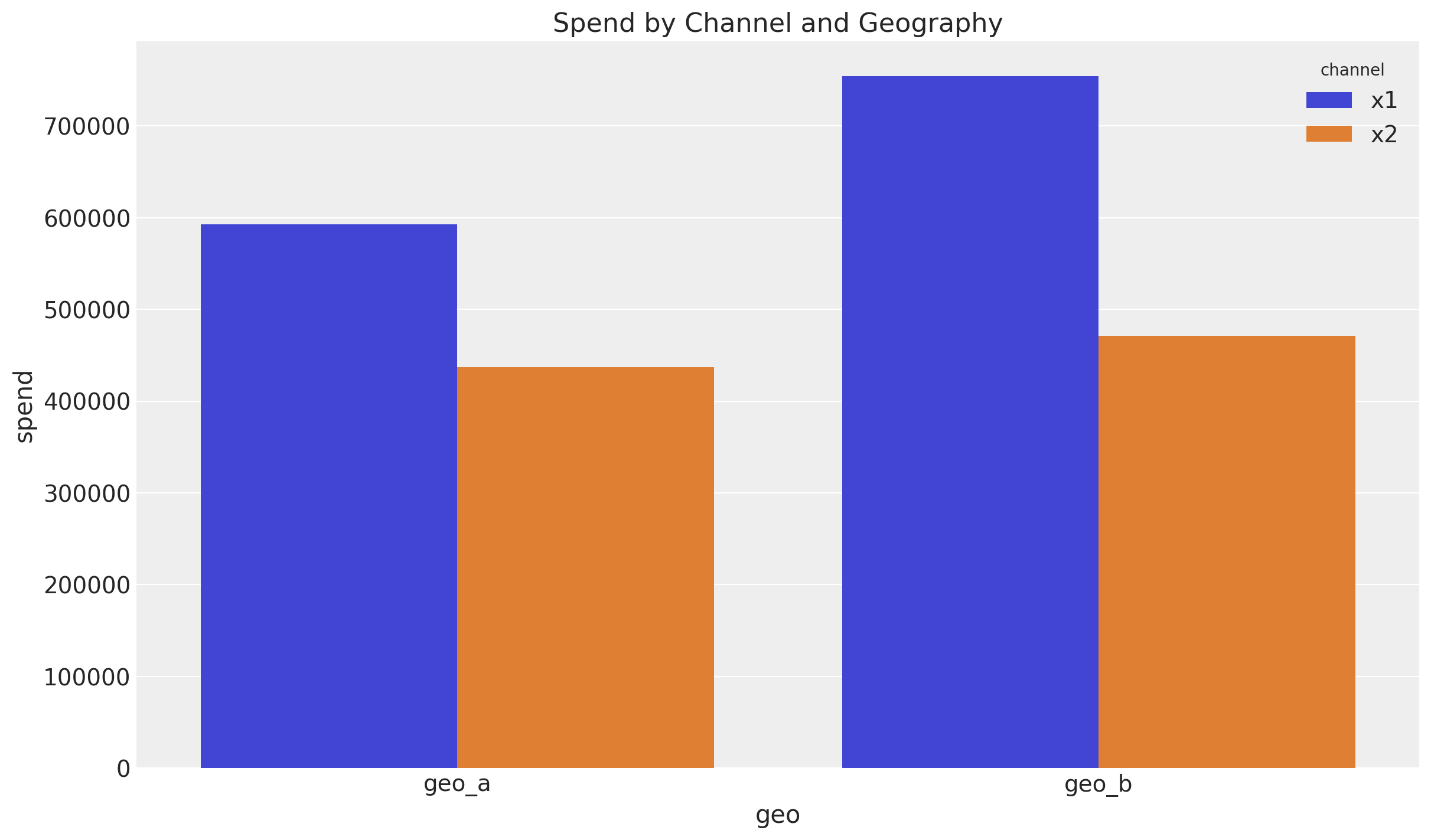
Let’s compute the spend share for each channel and geography.
fig, ax = plt.subplots()
(
data_df.melt(
id_vars=["geo", "date"],
value_vars=["x1", "x2"],
var_name="channel",
value_name="spend",
)
.groupby(["geo", "channel"], as_index=False)
.agg({"spend": "sum"})
.pipe((sns.barplot, "data"), x="geo", y="spend", hue="channel", ax=ax)
)
ax.set_title("Spend by Channel and Geography");
Model Specification and Fitting#
We’ll fit a multi-dimensional MMM with:
Geometric Adstock: Models the carry-over effect of advertising
Logistic Saturation: Models diminishing returns as spend increases
For simplicity, we use a streamlined model configuration.
# Define adstock and saturation transformations
adstock = GeometricAdstock(
priors={"alpha": Prior("Beta", alpha=2, beta=5, dims=("geo", "channel"))},
l_max=8,
)
saturation = LogisticSaturation(
priors={
"beta": Prior("Gamma", mu=0.3, sigma=0.15, dims=("geo", "channel")),
"lam": Prior("Gamma", mu=0.5, sigma=0.25, dims="channel"),
}
)
# Model configuration
model_config = {
"intercept": Prior("Gamma", mu=0.5, sigma=0.25, dims="geo"),
"gamma_control": Prior("Normal", mu=0, sigma=0.5, dims="control"),
"likelihood": Prior(
"TruncatedNormal",
lower=0,
sigma=Prior("HalfNormal", sigma=1.5),
dims=("date", "geo"),
),
}
# Create the MMM instance
mmm = MMM(
date_column="date",
target_column="y",
channel_columns=["x1", "x2"],
control_columns=["event_1", "event_2"],
dims=("geo",),
scaling={
"channel": {"method": "max", "dims": ()},
"target": {"method": "max", "dims": ()},
},
adstock=adstock,
saturation=saturation,
yearly_seasonality=2,
model_config=model_config,
)
Now we fit the model.
# Prepare training data
x_train = data_df.drop(columns=["y"])
y_train = data_df["y"]
# Build and fit the model
mmm.build_model(X=x_train, y=y_train)
# Add original scale contribution variables (needed for original_scale=True in plots)
mmm.add_original_scale_contribution_variable(var=["channel_contribution", "y"])
sample_kwargs = {
"draws": 1_500,
"tune": 1_000,
"chains": 4,
"target_accept": 0.85,
"nuts_sampler": "nutpie",
"random_seed": rng,
}
# Fit the model
mmm.fit(
X=x_train,
y=y_train,
**sample_kwargs,
)
# Sample posterior predictive
_ = mmm.sample_posterior_predictive(X=x_train, random_seed=rng)
Sampler Progress
Total Chains: 4
Active Chains: 0
Finished Chains: 4
Sampling for now
Estimated Time to Completion: now
| Progress | Draws | Divergences | Step Size | Gradients/Draw |
|---|---|---|---|---|
| 2500 | 0 | 0.39 | 15 | |
| 2500 | 0 | 0.42 | 15 | |
| 2500 | 0 | 0.39 | 15 | |
| 2500 | 0 | 0.46 | 7 |
Sampling: [y]
# Quick check of model diagnostics
print(f"Divergences: {mmm.idata.sample_stats.diverging.sum().values}")
Divergences: 0
We have no divergences!
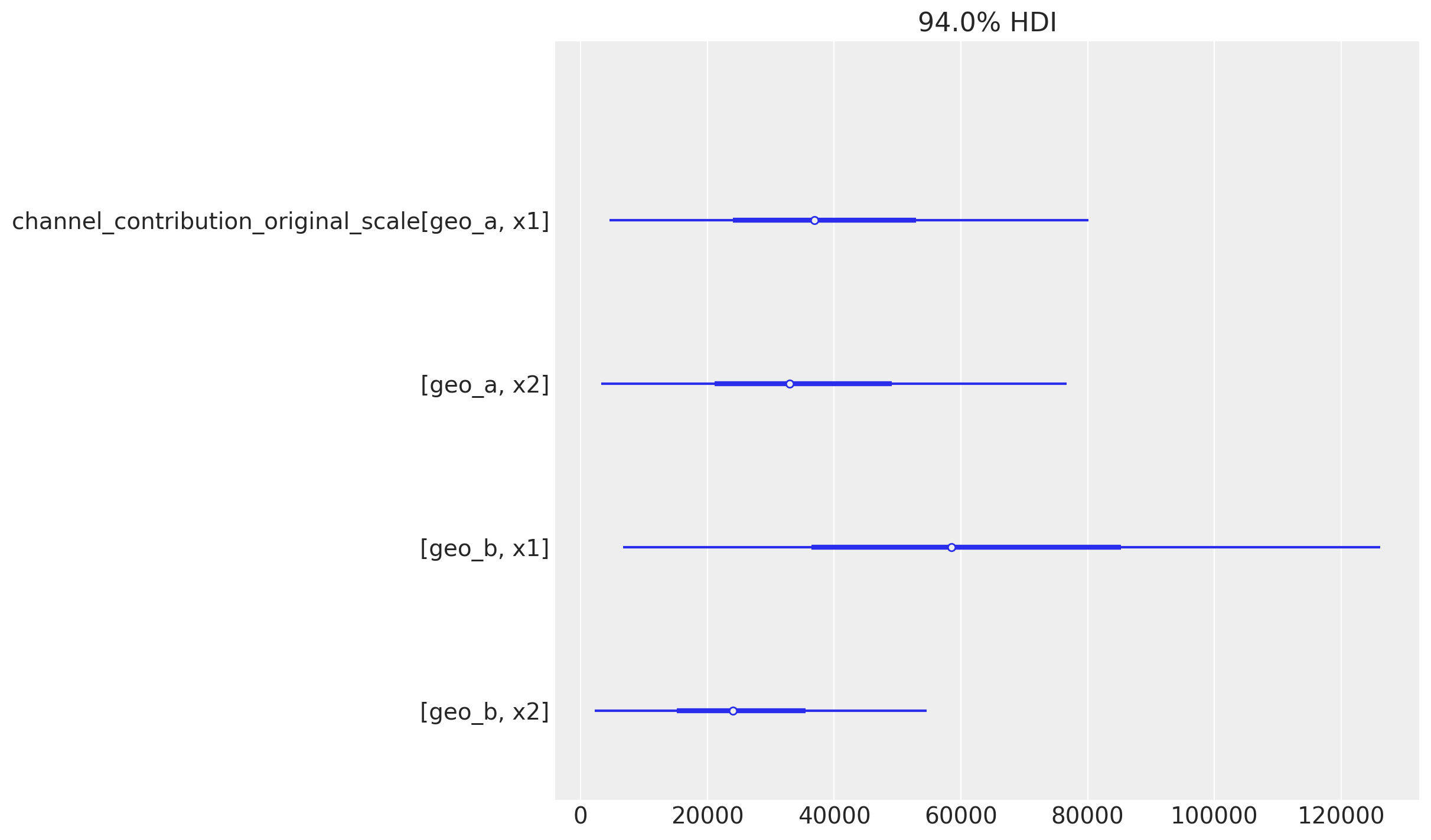
We can continue by looking into the aggregated contribution posterior of each channel.
fig, ax = plt.subplots()
az.plot_forest(
mmm.fit_result["channel_contribution_original_scale"].sum(dim="date"),
combined=True,
ax=ax,
);
For Geo A, we see that the contribution of \(x_1\) and \(x_2\) are comparable whereas for Geo B, \(x_1\) has a much higher contribution than \(x_2\).
This is a great start, but we want to understand better these contributions and how they are related by the current spend levels.
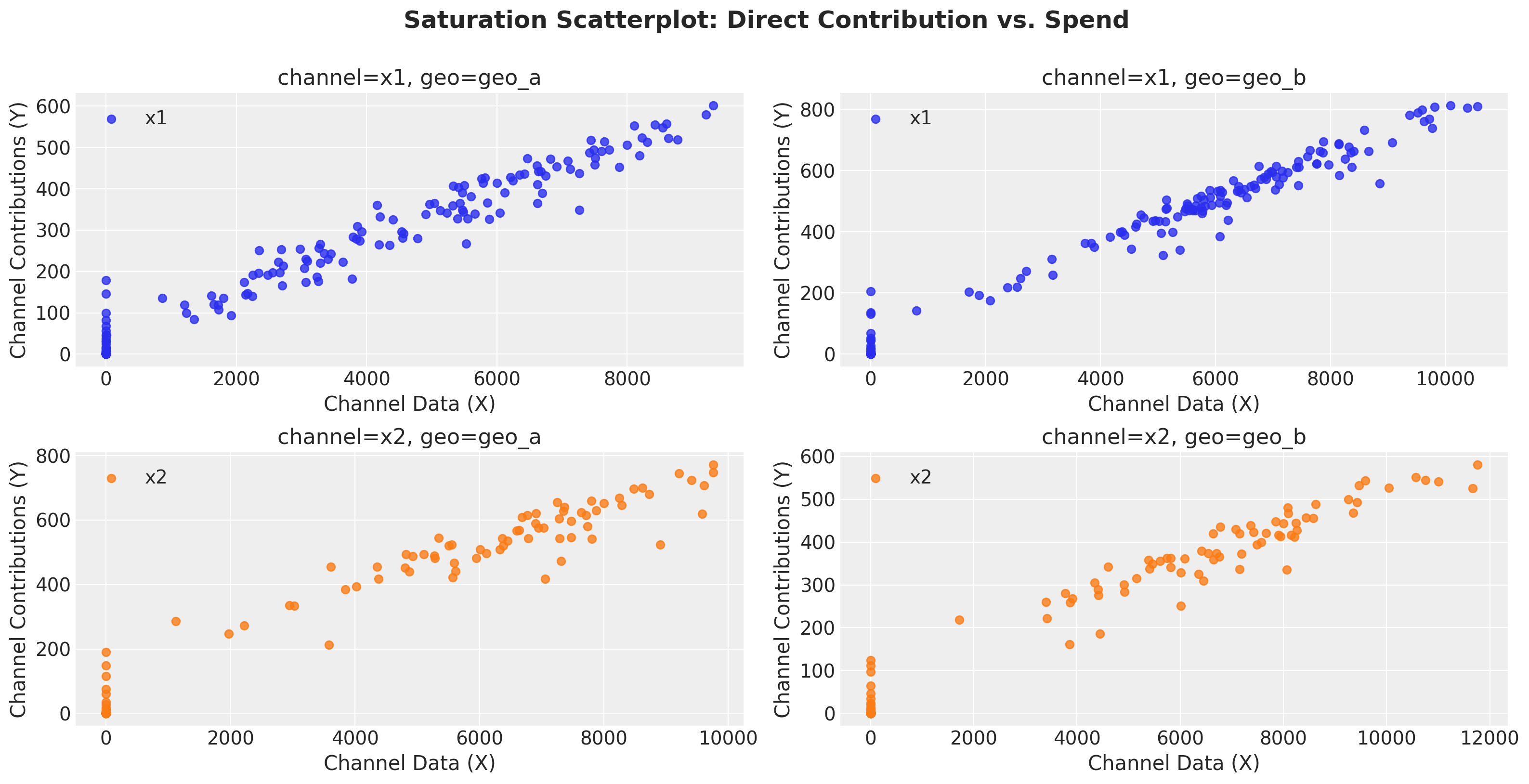
Visualization 1: Direct/Marginal Contribution#
The saturation_scatterplot shows the direct relationship between spend and contribution at each time point. This visualization answers the question:
“Given a specific spend level, what is the direct contribution to sales?”
Each point in this plot represents a single observation (one time period), showing:
X-axis: Channel spend at that time point
Y-axis: Direct contribution to sales at that time point
fig, axes = mmm.plot.saturation_scatterplot(
width_per_col=8,
height_per_row=4,
original_scale=True,
)
fig.suptitle(
"Saturation Scatterplot: Direct Contribution vs. Spend",
fontsize=18,
fontweight="bold",
y=1.01,
)
plt.tight_layout()
/var/folders/cm/3dzy9rdd5s3672z0s1brjkvh0000gn/T/ipykernel_24206/1864980976.py:12: UserWarning: The figure layout has changed to tight
plt.tight_layout()
How to interpret this plot:
Shape of the curve: The fitted line shows how contribution increases with spend, with diminishing returns visible as the curve flattens at higher spend levels.
Scatter points: Each point represents a specific date’s spend-contribution pair.
Note
This plot shows the instantaneous/marginal relationship. It tells you “if I spend X on a given day, I expect Y contribution on that day.”
The reason you see non-zero contribution even at zero spend is because of the adstock effect.
Tip
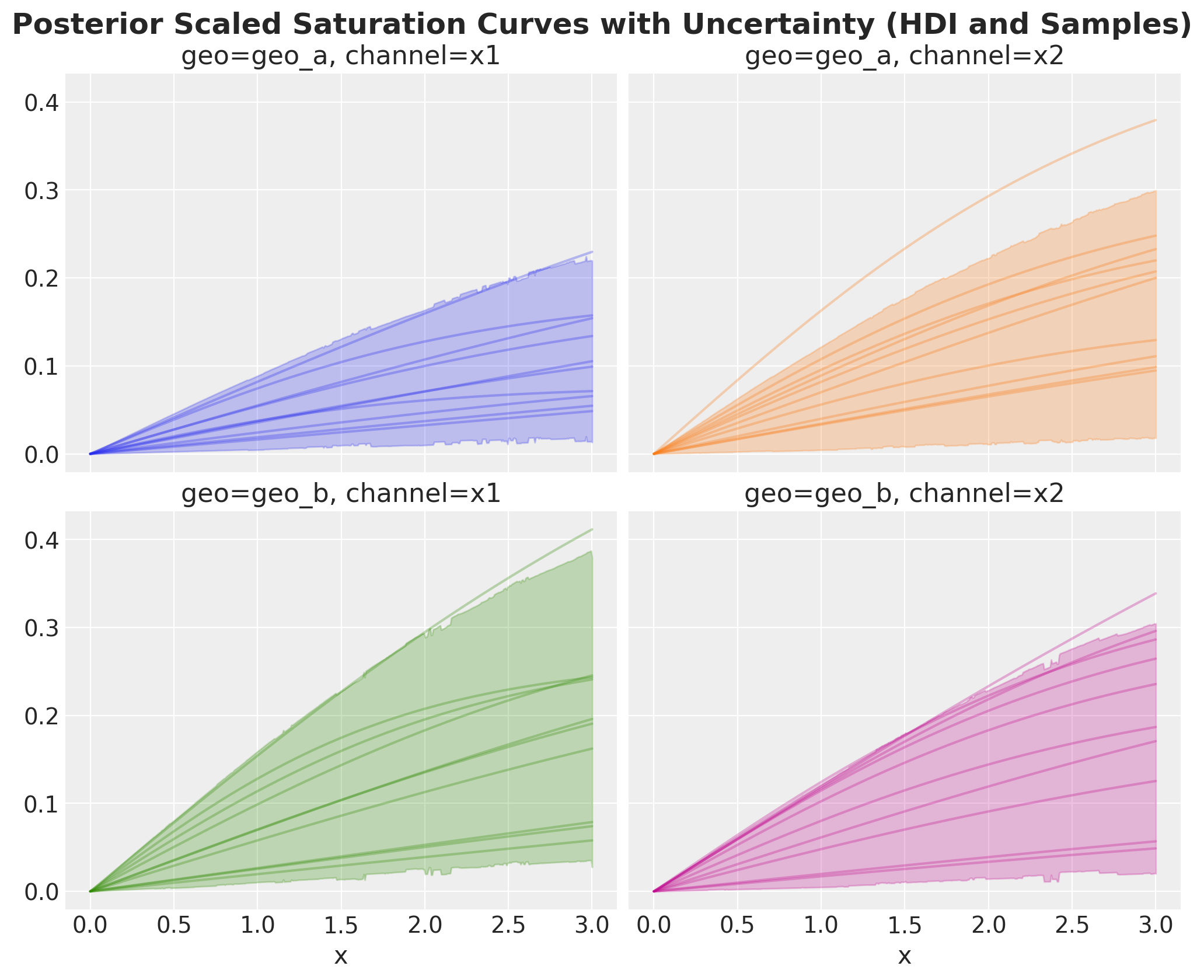
We can plot the posterior saturation curves for each channel and geography using the mmm.saturation.sample_curve method (please note you need to pass the whole posterior inference data!).
As we are internally scaling data data, these plots are in the scaled space. They are still useful to compare relative behavior across channels and geographies.
posterior_curve = mmm.saturation.sample_curve(
mmm.idata["posterior"], num_points=500, max_value=3
)
# Plot the saturation curve with uncertainty (HDI and samples)
_, axes = plt.subplots(
nrows=2,
ncols=2,
figsize=(10, 8),
sharex=True,
sharey=True,
layout="constrained",
)
fig, axes = saturation.plot_curve(posterior_curve, axes=axes, random_seed=rng)
fig.suptitle(
"Posterior Scaled Saturation Curves with Uncertainty (HDI and Samples)",
fontsize=18,
fontweight="bold",
y=1.03,
);
Sampling: []
Visualization 2: Total Contribution over Spend Share#
The sensitivity_analysis shows how total contribution (summed over all time periods) changes as you scale overall spend. This visualization answers the question:
“If I increase/decrease my total budget by X%, what is the total impact on sales?”
This is a counterfactual analysis: we ask “what would have happened if we had spent more or less?”
# Here we set scenarios to sweep over
# a 10% to 200% of the historical spend.
sweeps = np.linspace(0.1, 2.0, 100)
mmm.sensitivity.run_sweep(
sweep_values=sweeps,
var_input="channel_data",
var_names="channel_contribution_original_scale",
extend_idata=True, # it could be false and you save the object
)
/Users/juanitorduz/Documents/pymc-marketing/pymc_marketing/mmm/sensitivity_analysis.py:146: FutureWarning: The return type of `Dataset.dims` will be changed to return a set of dimension names in future, in order to be more consistent with `DataArray.dims`. To access a mapping from dimension names to lengths, please use `Dataset.sizes`.
draws = int(self.idata.posterior.dims.get("draw", 0))
<frozen _collections_abc>:811: FutureWarning: The return type of `Dataset.dims` will be changed to return a set of dimension names in future, in order to be more consistent with `DataArray.dims`. To access a mapping from dimension names to lengths, please use `Dataset.sizes`.
Let’s plot the results:
fig, axes = mmm.plot.sensitivity_analysis(
xlabel="Sweep multiplicative",
ylabel="Total contribution over training period",
hue_dim="channel",
subplot_kwargs={"nrows": 2, "figsize": (12, 10)},
)
for ax in axes.flat:
ax.axvline(1.0, color="black", linestyle="--", linewidth=1)
/Users/juanitorduz/Documents/pymc-marketing/pymc_marketing/mmm/plot.py:2520: UserWarning: The figure layout has changed to tight
fig.tight_layout()
How to interpret this plot:
X-axis (sweep multiplicative): The spend multiplier. A value of 1.0 represents the actual historical spend, 0.5 means half the spend, and 2.0 means double the spend.
Y-axis (Total Contribution): The sum of contributions across all time periods in the dataset.
Vertical line at sweep=1: This marks the current/historical spend level.
HDI bands: Show the uncertainty in total contribution at each spend level.
Curve shape:
Steep slope at low sweep → High marginal returns (you’re not yet saturated)
Flattening slope at high sweep → Diminishing returns (approaching saturation)
Important
This plot shows the global/total relationship. It tells you “across the entire time period, if I had scaled all my spend by factor “sweep”, my total contribution would be Y.”
Observe, that these results are consistent with the initial total copntribution analysis: For Geo A, \(x_1\) and \(x_2\) have similar contributions, but for Geo B, \(x_1\) has a much higher contribution than \(x_2\) (at the current spend levels).
Advanced Usage#
The plot.sensitivity_analysis method supports several advanced options for customization.
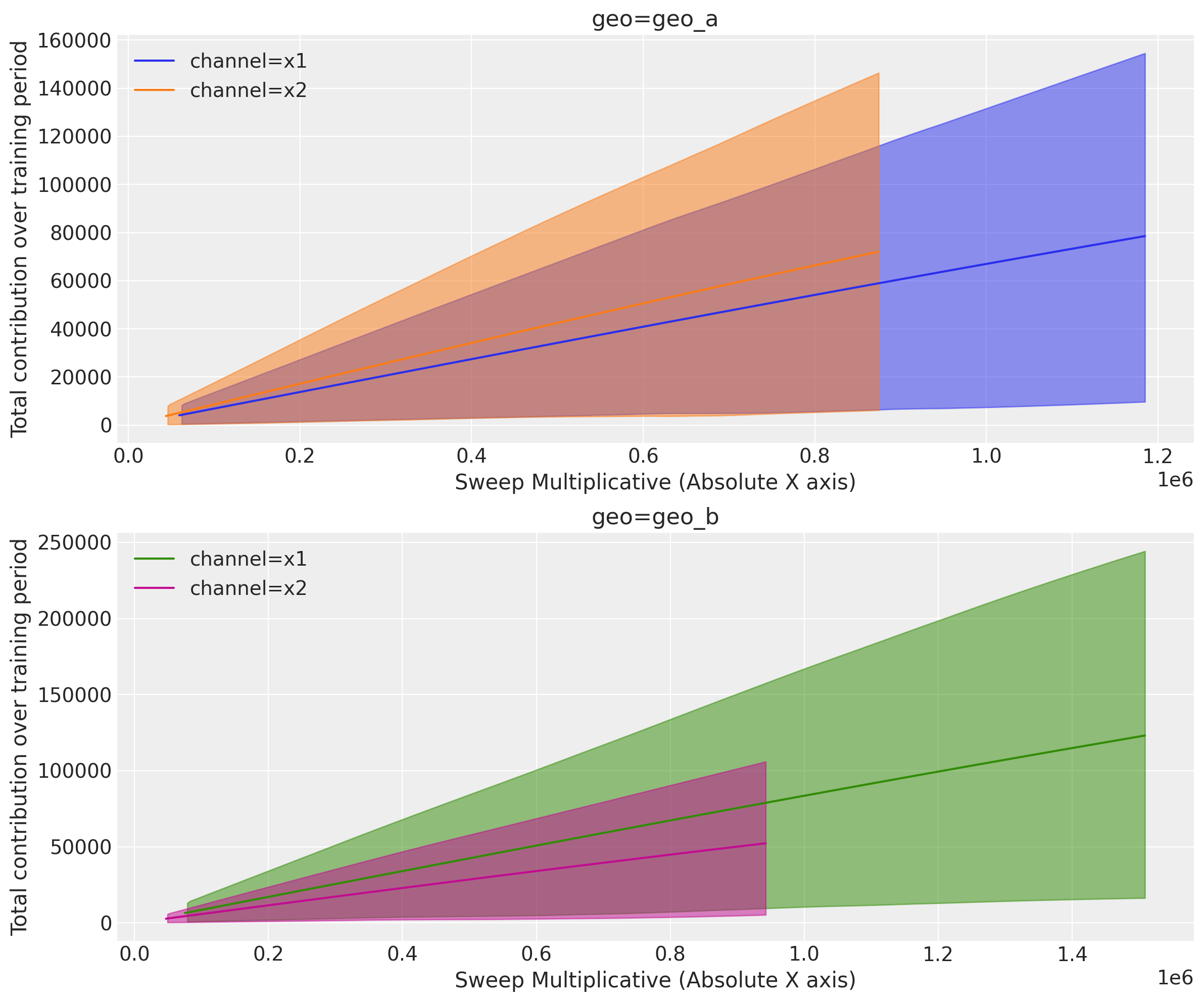
Using Absolute X-Axis#
Instead of showing the sweep multiplier on the x-axis, you can display absolute spend values using x_sweep_axis="absolute". This multiplies the sweep values by the channel_scale for each channel, so each line shows its actual spend range.
Note: When using x_sweep_axis="absolute":
Each channel will have its own X-axis range based on its scale factor
For example, if channel A has scale 500K and channel B has scale 2M, at sweep=2x:
Channel A shows values up to 1M (500K x 2)
Channel B shows values up to 4M (2M x 2)
This is useful for seeing actual spend values rather than relative multipliers
Requires
hue_dimto be set (typically “channel”)
Let’s first examine the sensitivity analysis data structure:
fig, axes = mmm.plot.sensitivity_analysis(
xlabel="Sweep Multiplicative (Absolute X axis)",
ylabel="Total contribution over training period",
hue_dim="channel",
x_sweep_axis="absolute",
subplot_kwargs={"nrows": 2, "figsize": (12, 10)},
)
/Users/juanitorduz/Documents/pymc-marketing/pymc_marketing/mmm/plot.py:2520: UserWarning: The figure layout has changed to tight
fig.tight_layout()
With x_sweep_axis="absolute":
The x-axis shows actual spend values (sweep multiplier x total spend over the training period)
Each channel has its own x-axis range based on its scale factor
This view is more intuitive for budget discussions (“If we spend X total, we get Y contribution”)
Note: Lines may end at different x-values since channels have different scales
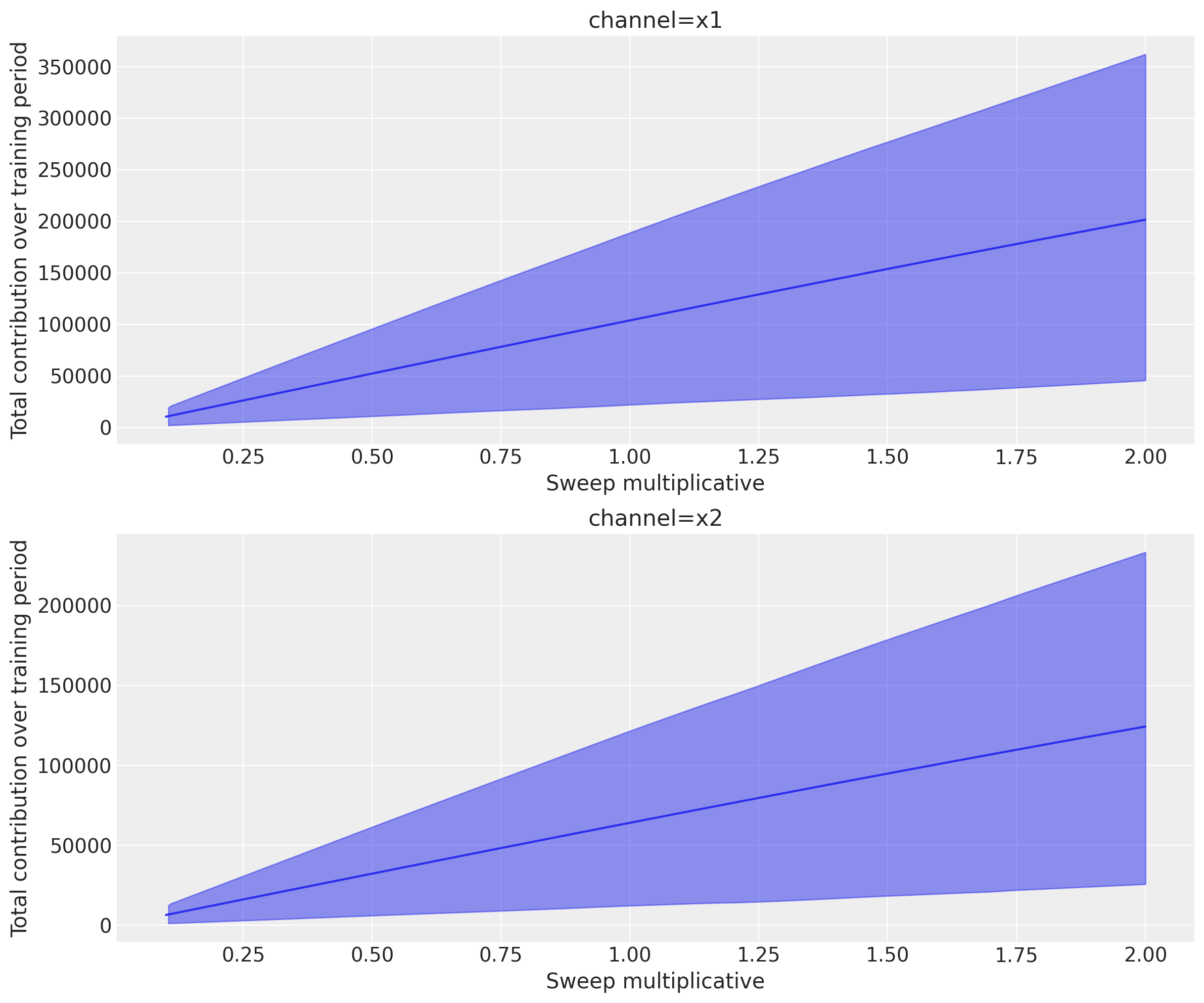
Filtering by Geography#
We can use xarray’s API to filter by geography.
channels_geo_a = mmm.idata.sensitivity_analysis.sel(geo="geo_a")
# Plot the mean line
channels_geo_a.mean(dim=["sample"]).x.plot(hue="channel")
# For HDI, iterate over channels and pass DataArrays
for index, channel in enumerate(channels_geo_a.coords["channel"].values):
az.plot_hdi(
x=channels_geo_a.coords["sweep"], # or whatever your x-axis coordinate is
y=channels_geo_a["x"].sel(channel=channel), # DataArray, not Dataset
hdi_prob=0.94,
color=f"C{index}",
)
/opt/homebrew/Cellar/micromamba/2.5.0/envs/pymc-marketing-env/lib/python3.13/site-packages/arviz/plots/hdiplot.py:166: FutureWarning: hdi currently interprets 2d data as (draw, shape) but this will change in a future release to (chain, draw) for coherence with other functions
hdi_data = hdi(y, hdi_prob=hdi_prob, circular=circular, multimodal=False, **hdi_kwargs)
/opt/homebrew/Cellar/micromamba/2.5.0/envs/pymc-marketing-env/lib/python3.13/site-packages/arviz/plots/hdiplot.py:166: FutureWarning: hdi currently interprets 2d data as (draw, shape) but this will change in a future release to (chain, draw) for coherence with other functions
hdi_data = hdi(y, hdi_prob=hdi_prob, circular=circular, multimodal=False, **hdi_kwargs)
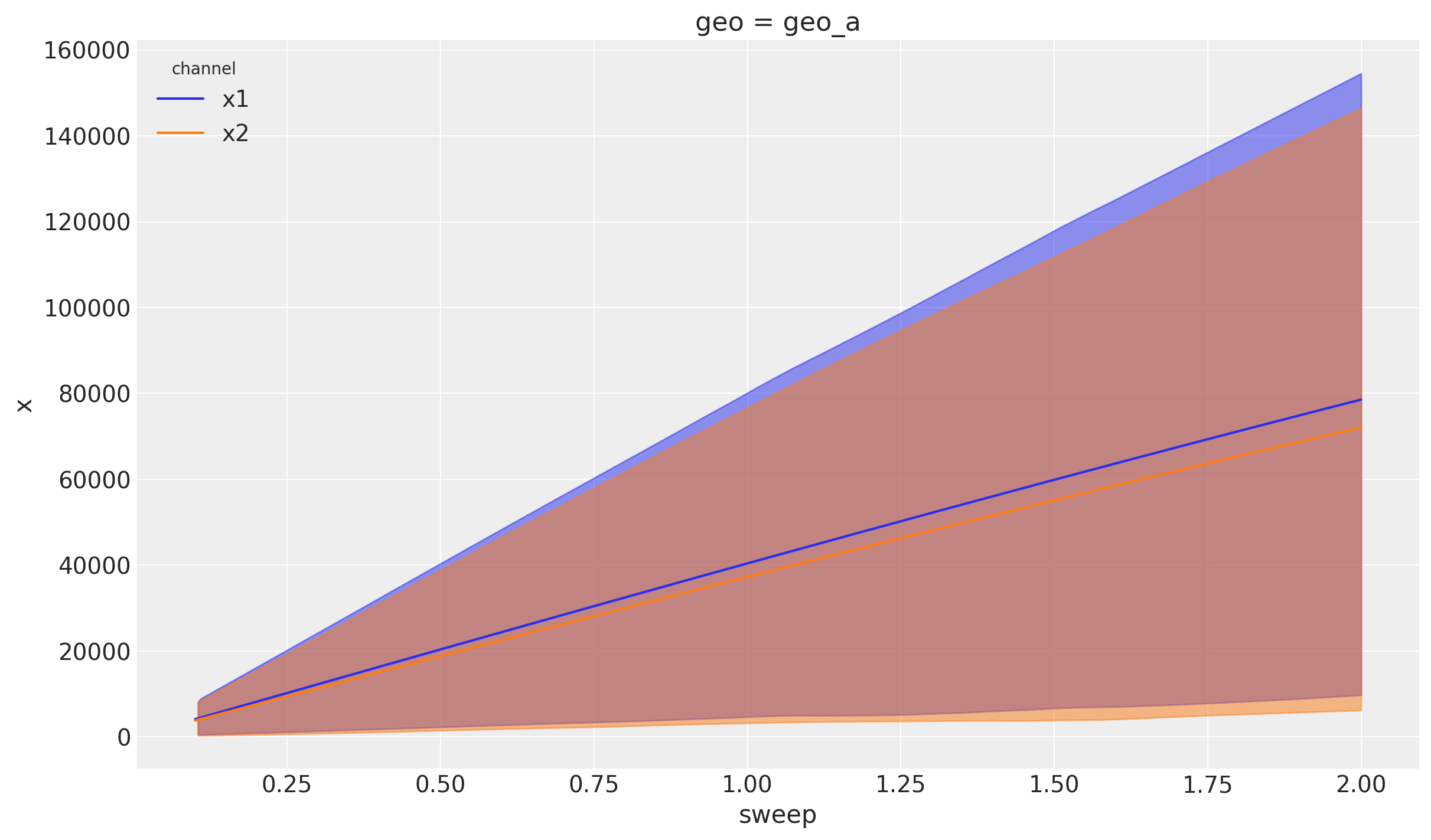
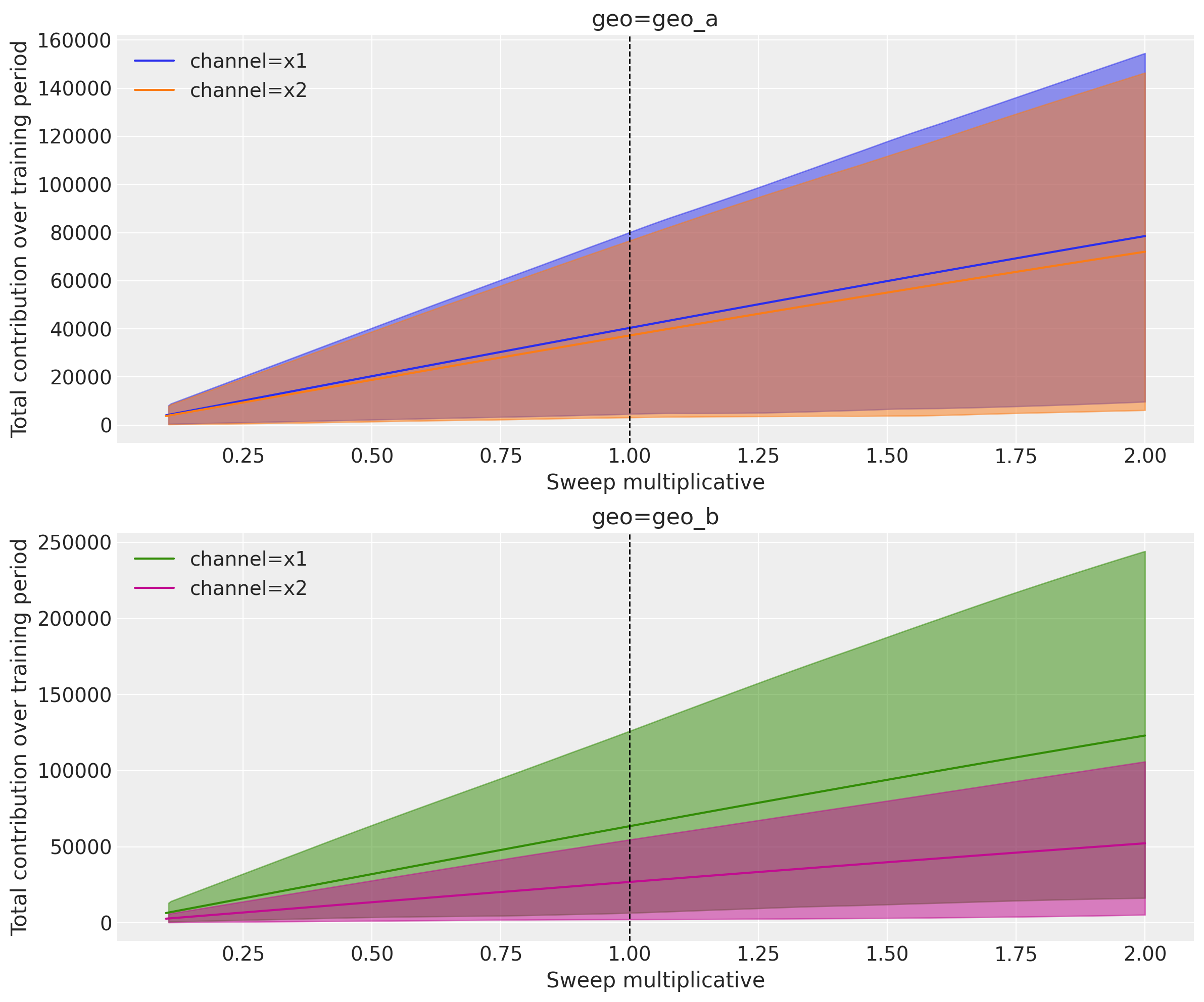
Aggregating Across Geographies#
Use the aggregation parameter to combine results across dimensions. This is useful when you want to see the total impact across all markets:
fig, axes = mmm.plot.sensitivity_analysis(
xlabel="Sweep multiplicative",
ylabel="Total contribution over training period",
aggregation={"sum": ("geo",)},
subplot_kwargs={"figsize": (12, 10), "nrows": 2},
)
/Users/juanitorduz/Documents/pymc-marketing/pymc_marketing/mmm/plot.py:2520: UserWarning: The figure layout has changed to tight
fig.tight_layout()
Supported aggregation operations:
"sum": Sum contributions across the specified dimensions"mean": Average contributions across the specified dimensions"median": Median contributions across the specified dimensions
Summary#
In this tutorial, we explored two complementary ways to visualize media saturation in Marketing Mix Models:
saturation_scatterplot: Shows the direct/marginal relationship between spend and contribution at each time point. Best for understanding the shape of saturation and validating model behavior.sensitivity_analysis: Shows how total contribution changes as you scale overall spend. Best for budget planning, what-if analysis, and making allocation decisions.
Understanding the difference between these visualizations is crucial for correctly interpreting your MMM results and making informed marketing decisions.
%load_ext watermark
%watermark -n -u -v -iv -w -p pymc_marketing
Last updated: Tue, 20 Jan 2026
Python implementation: CPython
Python version : 3.13.11
IPython version : 9.9.0
pymc_marketing: 0.17.1
arviz : 0.23.0
matplotlib : 3.10.8
numpy : 2.3.5
pandas : 2.3.3
preliz : 0.23.0
pymc_extras : 0.7.0
pymc_marketing: 0.17.1
seaborn : 0.13.2
Watermark: 2.6.0